1.2.2 Prédicat sur un ensemble. Sous-ensembles.

Définition 1.2.3 (Prédicat)
On appelle prédicat sur l'ensemble E une phrase p(x) qui devient une proposition lorsqu'on substitue à la lettre x un élément de E. Plus généralement, un prédicat à n variables $x_1 \in E_1,\,x_2 \in E_2,\ldots,\,x_n \in E_n$ est une phrase $p(x_1,x_2,\ldots,x_n)$ qui devient une proposition quand on remplace $x_1,x_2,\ldots,x_n$ par des éléments de $E_1,\,E_2,\ldots,\,E_n$.

Un prédicat est donc une phrase dont la valeur de vérité est variable : $p(x)$ est vraie quand on remplace $x$ par certains éléments de $E$, fausse pour les autres.^1.19

Exemples :

$p(x) \equiv$ « $x$ est un nombre rationnel » est un prédicat sur l'ensemble ${\mathbb{R}}$ des nombres réels.

« $x$ divise $y$ » $\equiv$ « $y$ est un multiple de $x$ » est un prédicat à deux variables sur l'ensemble ${\mathbb{Z}}$ des entiers relatifs.

Toutes les opérations définies sur les propositions s'appliquent évidemment aux prédicats sur un même ensemble. Par exemple $p(x) \oplus q(x)$ est un prédicat ; il est vrai pour $x=a$ si l'une des deux propositions $p(a)$ et $q(a)$, et une seulement, est vraie.

Définition 1.2.4 (Sous-ensemble d'un ensemble)
Soit E un ensemble. Un sous ensemble de E est un ensemble A tel que tout élément de A est élément de E. On écrit alors $A\subset E$. ^1.20On note $A \varsubsetneq E$ la proposition ( $A\subset E$) et ($A \neq E$).

On a alors les propriétés suivantes :

$A\subset E \equiv (x \in A \Longrightarrow x \in E)$.

Pour tout ensemble $E,\ \emptyset \subset E$ et $E \subset E$.^1.21.

$E=F \equiv (E \subset F)$ et $(F \subset E)$.

Exercice 1..10
Écrire tous les sous-ensembles de $\emptyset$, de $\{a\}$, de $\{a,b\}$ et de $\{a,b,c\}$.

Axiome 1.2.2 (Correspondance entre prédicats et sous-ensembles)
Soit p(x) un prédicat sur un ensemble E. Il existe un sous-ensemble A de E qui est exactement l'ensemble des $x \in E$ tels que p(x) soit vraie. on le note $A=\{x \in E / p(x)\}$.
Réciproquement, si A est un sous-ensemble de E, $A=\{x \in E / x \in A\}$.

Cet axiome, qui s'appelle l'axiome d'extensionalité, va nous permettre de traduire les définitions et théorèmes sur les propositions, et donc sur les prédicats, en définitions et opérations sur les ensembles.

Les opérations essentielles sont résumées dans le tableau 1.3.

Les propriétés de ces opérations sont énoncées dans le théorème 1.2.1.

Figure 1.3: Correspondance entre sous-ensembles et prédicats

Théorème 1.2.1
Soient A B C des sous-ensembles de E. On a les propriétés suivantes :^1.22

1. $(A^c)^c = A$.
2. Commutativité : $A \cap B = B \cap A$ et $A \cup B = B \cup A$.
3. Associativité : $A \cap (B \cap C)= (A \cap B) \cap C$ et $A \cup (B \cup C)= (A \cup B) \cup C$ : on notera donc $A \cap B \cap C$ et $A \cup B \cup C$ sans parenthèses.
4. $A \cap A = A = A \cup A$.
5. $A \cap A^c = \emptyset$ et $A \cup A^c = E$.
6. $A \cap \emptyset = \emptyset$ et $A \cup \emptyset = A$.
7. $A \cap E = A$ et $A \cup E = E$.
8. Distributivités : $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$ et $A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$ $\blacktriangleleft$

Exercice 1..11
Démontrez les propiétés 8 de distributivité de l'intersection sur la réunion et de la réunion sur l'intersection (appelées lois de De Morgan).

La décomposition d'une fonction logique en fonctions logiques élémentaires (minterms) a également sa traduction en termes de sous-ensembles d'un ensemble $E$. Nous l'énoncerons d'abord pour trois sous-ensembles :

Théorème 1.2.2 (sous-ensembles élémentaires à trois variables)
Soient A, B, C des sous-ensembles d'un ensemble E. Alors E est réunion des $2^3$ sous-ensembles deux à deux disjoints :

$$\begin{array}{cccc} A^c \cap B^c \cap C^c & A^c \cap B^c \ca... ...& A \cap B \cap C\\ (100) & (101) & (110) & (111) \end{array}$$

On les appelle sous-ensembles élémentaires (associés aux sous-ensembles A, B, C). Tout sous-ensemble de E s'exprimant à l'aide de A, B et C est réunion de sous-ensembles élémentaires.

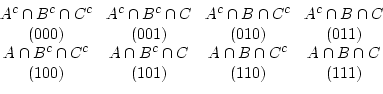
Les nombres binaires entre parenthèses représentent les valeurs de verité du triplet ($x \in A$ , $x \in B$ , $x \in C$).

Il est commode de représenter ces sous-ensembles par des régions du plan.

Figure 1.4: Sous-ensembles élémentaires associés à trois sous-ensembles.

Ce dessin^1.23 peut être trompeur : certaines régions représentées peuvent être vides. Par exemple si $A \subset B$, les régions $A \cap B^c \cap C^c$ et $A \cap B^c \cap C$ (100 et 101) sont vides.

Exercice 1..12
Sans utiliser l'exercice 1.6, décomposez $A \oplus (B \oplus C)$ en sous-ensembles élémentaires. En déduire que $A \oplus (B \oplus C) = (A \oplus B) \oplus C$.

Théorème 1.2.3 (sous-ensembles élémentaires à n variables)
Soient $A_1,A_2,\ldots,A_n$ des sous-ensembles d'un ensemble E. E est réunion des $2^n$ sous-ensembles deux à deux disjoints :

$A_1^c \cap A_2^c \cap \cdots \cap A_{n-1}^c \cap A_n^c \qquad A_1^c \cap A_2^c... ...\cap A_{n-1} \cap A_n^c\ \ldots\ A_1 \cap A_2 \cap \cdots \cap A_{n-1} \cap A_n$

c'est-à-dire des ensembles de la forme $A_1^\prime \cap A_2^\prime \cap \cdots \cap A_{n-1}^\prime \cap A_n^\prime$

avec $A_1^\prime = A_1$ ou $A_1^\prime = A_1^c$, $A_2^\prime = A_2$ ou $A_2^\prime = A_2^c$, ..., $A_n^\prime = A_n$ ou $A_n^\prime = A_n^c$.
Tout sous-ensemble de $E$ fonction de $A_1,A_2,\ldots,A_n$ est réunion de tels sous-ensembles élémentaires.

Exercice 1..13

1. En utilisant l'exercice 1.12, décomposer $(A \oplus B \oplus C)^c$ en sous-ensembles élémentaires.
2. En déduire la décomposition de $A \oplus B \oplus C \oplus D$ et de $(A \oplus B \oplus C \oplus D)^c$ en sous-ensembles élémentaires.