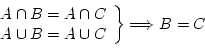suivant: Les nombres monter: 1.2 Ensembles précédent: 1.2.2 Prédicat sur un ensemble. Sous-ensembles.

«
![]() » s'écrit aussi «
» s'écrit aussi «
![]() », ou «
», ou «
![]() »,
ou encore « tout élément de
»,
ou encore « tout élément de ![]() vérifie
vérifie ![]() »; ce n'est pas un prédicat dont la valeur de vérité dépend
d'une variable, mais une proposition vraie ou fausse ;
la lettre
»; ce n'est pas un prédicat dont la valeur de vérité dépend
d'une variable, mais une proposition vraie ou fausse ;
la lettre ![]() (ou
(ou ![]() ou
ou ![]() ) n'y figure pas vraiment, en ce sens qu'elle ne désigne pas un objet déterminé
1.24.
) n'y figure pas vraiment, en ce sens qu'elle ne désigne pas un objet déterminé
1.24.
Exemple :
Soit ![]() le prédicat «
le prédicat « ![]() est mortel » sur l'ensemble
est mortel » sur l'ensemble ![]() des êtres humains. «
des êtres humains. «
![]() » est la proposition
« Tout humain est mortel » (Platon).
» est la proposition
« Tout humain est mortel » (Platon).
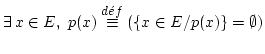
Les propositions «
![]() » et «
» et «
![]() » s'appellent des propositions quantifiées : on y compte
(quantifie) les éléments de E vérifiant la propriété
» s'appellent des propositions quantifiées : on y compte
(quantifie) les éléments de E vérifiant la propriété ![]() .
.
Démonstration :
Il est clair que
![]() . Si l'ensemble
. Si l'ensemble
![]() est différent de
est différent de ![]() , son
complémentaire dans
, son
complémentaire dans ![]() , qui est égal à
, qui est égal à
![]() , n'est pas vide, donc contient un élement au moins.
, n'est pas vide, donc contient un élement au moins.
Exemple :
La négation de « Tout humain est mortel » est « Il existe au moins un humain immmortel », et non pas « Tout humain est immortel », ni « Tout non humain est immortel », ni « Il existe un non humain immortel »: pour prouver que « Tout humain est mortel » est une proposition fausse, il faut trouver une exception, un humain non mortel. En mathématiques, une telle exception s'appelle un contre-exemple (voir 1.2.3).
Pour trouver la négation d'une proposition quantifiée, on remplace donc mécaniquement ![]() par
par ![]() , et vice versa, et
le prédicat qui suit par sa négation. Mais ceci ne dispense pas de réfléchir au sens de ces propositions, comme le montre l'exemple
précédent.
, et vice versa, et
le prédicat qui suit par sa négation. Mais ceci ne dispense pas de réfléchir au sens de ces propositions, comme le montre l'exemple
précédent.
Remarques sur cet exercice:
La proposition p est fausse : ![]() fournit un contre-exemple.
fournit un contre-exemple.
La proposition ![]() affirme que
affirme que ![]() est la limite de la suite
est la limite de la suite
![]() : elle dit que pour
: elle dit que pour ![]() assez grand
(
assez grand
(
![]() ),
), ![]() est aussi proche que l'on veut de
est aussi proche que l'on veut de ![]() (
(
![]() ). Sa négation affirme qu'il existe un
). Sa négation affirme qu'il existe un
![]() tel que, même si
tel que, même si ![]() est grand, il y a au moins un
est grand, il y a au moins un ![]() plus grand (
plus grand (![]() ) pour lequel
) pour lequel ![]() est loin de
est loin de ![]() (
(
![]() ). Mais il n'est pas indispensable de savoir cela pour écrire la négation de
). Mais il n'est pas indispensable de savoir cela pour écrire la négation de ![]() .
.
Tout ce qui précède nous permet de distinguer trois types de raisonnement en mathématiques :
Le raisonnement par déduction :
Pour démontrer le théorème
![]() , on suppose que
, on suppose que ![]() vérifie l'hypothèse
vérifie l'hypothèse ![]() , et on en déduit
que la conclusion
, et on en déduit
que la conclusion ![]() est vraie.
est vraie.
Le raisonnement par l'absurde :
Pour démontrer la proposition
![]() , qui est identique à
, qui est identique à
![]() 1.26,
on suppose que
1.26,
on suppose que ![]() ne vérifie pas la conclusion
ne vérifie pas la conclusion ![]() , et on en déduit une contradicion avec l'hypothèse
, et on en déduit une contradicion avec l'hypothèse ![]() .
.
Le raisonnement par contre-exemple :
Pour démontrer que la proposition
![]() est fausse, c'est-à-dire que
est fausse, c'est-à-dire que
![]() .
.
![]() est vraie, on cherche un
est vraie, on cherche un ![]() - un contre-exemple - vérifiant
- un contre-exemple - vérifiant ![]() et ne vérifiant pas
et ne vérifiant pas ![]() .
.
Il existe un quatrième mode de raisonnement, le raisonnement par récurrence, que nous verrons au chapitre suivant.
Dans cet exercice on n'a pas précisé l'ensemble de référence pour les prédicats. Il s'agit de l'ensemble
![]() des sous-ensembles d'un ensemble
des sous-ensembles d'un ensemble ![]() . La première proposition s'écrirait alors
. La première proposition s'écrirait alors
![]() . On évitera si possible
es notations si lourdes.1.27
. On évitera si possible
es notations si lourdes.1.27