Un ensemble est une collection d'objets appelés éléments de l'ensemble. Si 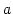 est un élement de l'ensemble
est un élement de l'ensemble 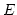 on
écrit
on
écrit
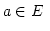 ou
ou
ce qui se lit « 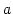 appartient à
appartient à 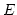 » ou «
» ou « 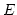 contient l'élement
contient l'élement 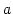 '' ou « a est un élément de E ».
On note «
'' ou « a est un élément de E ».
On note «
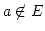 » la négation de «
» la négation de « 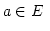 ».
».
Ceci n'est évidemment pas une définition correcte : un ensemble est une collection, une collection est un ensemble... Qu'est-ce
qu'un objet élément d'un ensemble ? En fait, les ensembles sont les objets dont on s'occupe en mathématiques,1.15 comme les
propositions sont les objets dont on s'occupe en logique, les termes primitifs de la théorie. Nous en resterons à un niveau
plus terre à terre.
On peut se réprésenter un ensemble comme une liste d'objets, ou comme une boîte contenant des objets ; mais ceci ne remplace pas une
définition correcte.
Un ensemble est défini :
- Par la liste de ses éléments (on dit en extension). On note alors
 , par exemple
, par exemple
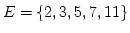 ,
,

- Par une propriété caractérisant ses éléments (on dit en compréhension). On note alors {x/x vérifie p},
ce qui se lit « l'ensemble des x vérifiant p », ou « l'ensemble des x tels que p soit vraie », par exemple
 est un entier positif, premier, et
est un entier positif, premier, et
.
Intuitivement, deux ensembles sont égaux s'ils ont les mêmes éléments.
Exemples :
- Les ensembles
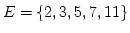 et
et
 est un entier positif, premier, et
est un entier positif, premier, et sont égaux.
sont égaux.
-
 : ce n'est pas parce qu'un élément est cité deux fois dans la liste que le contenu de la boîte change.
: ce n'est pas parce qu'un élément est cité deux fois dans la liste que le contenu de la boîte change.
Définition 1.2.1 (Ensemble vide)
Il existe un ensemble appelé ensemble vide, noté 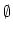 1.16,
qui ne contient aucun élément.1.17
1.16,
qui ne contient aucun élément.1.17
L'ensemble vide peut se représenter par une boîte vide.
Définition 1.2.2 (ensemble à un ou deux éléments)
L'ensemble dont le seul élément est a s'appelle l'ensemble réduit à a, ou le singleton a et se note {a}.
L'ensemble dont les éléments sont a,b ( ) se note {a,b}.
) se note {a,b}.
Exemples :
- {
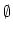 } à ne pas confondre avec
} à ne pas confondre avec 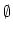 : une boîte contenant une boîte vide contient un élément.
: une boîte contenant une boîte vide contient un élément.
-
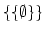 : une boîte contenant une boîte contenant une boîte vide.
: une boîte contenant une boîte contenant une boîte vide.
-
 : une boîte contenant une boîte contenant une boîte contenant une boîte vide.
: une boîte contenant une boîte contenant une boîte contenant une boîte vide.
-
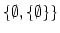 : une boîte contenant :
: une boîte contenant :
- une boîte vide
- une boîte contenant une boîte vide.
Les deux « définitions » précédentes permettent déjà de définir bon nombre d'ensembles.1.18 Il manque plusieurs axiomes, en particulier
l'axiome de l'infini, qui affirme qu'il existe un ensemble infini.
J.Rodary
1998-20?? : tant qu'y'a d'la vie y'a de l'espoir :-)
![]() est un élement de l'ensemble
est un élement de l'ensemble ![]() on
écrit
on
écrit