suivant: 2.4.3 Propriétés de monter: 2.4 Les nombres Complexes précédent: 2.4.1 Introduction
On appelle nombre complexe un couple
![]() de nombres réels.
On note
de nombres réels.
On note
![]() l'ensemble des nombres complexes.
On a donc
l'ensemble des nombres complexes.
On a donc
![]()
![]() 2.16.
2.16.

Commentaire : Avec cette définition, un nombre complexe
 n'est donc rien d'autre qu'un vecteur (libre)
n'est donc rien d'autre qu'un vecteur (libre)
 du plan
du plan
![]()
![]() (on note les vecteurs en colonne pour utiliser les notations du calcul matriciel),
ou encore un point
(on note les vecteurs en colonne pour utiliser les notations du calcul matriciel),
ou encore un point
 de
de
![]()
![]() .
.
On préfère habituellement faire la distinction entre le nombre complexe
 , le point
, le point

![]() et le vecteur
et le vecteur

![]() . Pour cela
. Pour cela
![]() s'appelle l'affixe de
s'appelle l'affixe de ![]() et de
et de ![]() .
.
![]() s'appelle l'image et
s'appelle l'image et ![]() le vecteur image de
le vecteur image de ![]() . L'affixe d'un point ou d'un vecteur s'écrit entre parenthèses, à droite de
ce point ou de ce vecteur.
. L'affixe d'un point ou d'un vecteur s'écrit entre parenthèses, à droite de
ce point ou de ce vecteur.
Pour
 et
et
 on définit leur somme par :
on définit leur somme par :


Cette définition n'est rien d'autre que la définition de la somme de deux vecteurs par la règle du parallélogramme, dont la justification - expérimentale - vient de l'étude de la résultante de deux forces.
La définition de la multiplication qui suit n'a plus rien à voir quant à elle avec la géométrie ou la mécanique. Elle est directement issue du problème algébrique initial : résoudre les équations du second degré sans racines reéelles.
 et
et
 on définit leur produit par :
on définit leur produit par :

Appliquant ces définitions aux nombres complexes de la forme
![]() pour
pour
![]() on obtient :
on obtient :
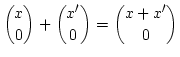 et
et 
On retrouve, sur la première composante, l'addition et la multiplication des réels. Si on identifie
![]() avec
avec
![]() l'addition et la multiplication dans
l'addition et la multiplication dans
![]() prolongent celles de
prolongent celles de
![]() . On posera donc
. On posera donc

On a alors
![]() . De plus
. De plus
 |
|||
 |

 sont les vecteurs de la base canonique de
sont les vecteurs de la base canonique de
En posant
 on obtient donc pour
on obtient donc pour
![]()

![]() s'appelle la partie réelle de
s'appelle la partie réelle de ![]() et se note
et se note
![]()
![]() s'appelle la partie imaginaire de
s'appelle la partie imaginaire de ![]() et se note
et se note
![]()
Si
![]() est nul,
est nul, ![]() est réel.
Si
est réel.
Si
![]() est nul, on dit que
est nul, on dit que ![]() est imaginaire pur.
Deux nombres complexes
est imaginaire pur.
Deux nombres complexes ![]() et
et
![]() sont égaux SSI
sont égaux SSI ![]() et
et ![]() : c'est la définition de
l'égalité de deux couples.
: c'est la définition de
l'égalité de deux couples.
On a
![]() et
et
Les sommes et les produits se calculent donc comme dans
![]() en remplašant
en remplašant ![]() par -1.
par -1.
J.Rodary